الخطوط العريضة للقسم
-
Le calcul fractionnaire est une extension du calcul différentiel et intégral traditionnel qui permet de généraliser les concepts de dérivation et d'intégration a des ordres non-entières. Cette théorie permet également de représenter de manière plus précise les phénomènes physiques ou biologiques qui ne suivent pas une évolution linaire ou continue.
Le calcul fractionnaire trouve des applications dans divers domaines, tels que la physique, la mécanique des fluides, la biologie, l'économie et la finance. Les équations différentielles fractionnaires sont utilisées pour modéliser des phénomènes tels que la diffusion des fluides, la propagation des ondes, la croissance de populations, les processus de filtration, l'analyse des signaux, la dynamique de marche, etc.
Les équations différentielles fractionnaires peuvent être classées selon différents critères : linéaires ou non-linéaires, a coefficients constants ou variables, a une ou plusieurs variables, etc. La résolution de ces équations peut être réalisée a` l'aide de différentes méthodes, telles que la méthode de variation de la constante, la méthode de Laplace, la méthode de la transformée de Fourier, décomposition d'Adomian ou la méthode de la perturbation d'homotopie.

-
Nouvelles diverses et annonces

-
-
Equations differentielles fractionnaires, cours Master2 mathématiques.
Semester : 03
Coefficient : 03
Credit : 06

-
Dr. Belmahi Naziha
University of science and technology Oran M-B
Faculty of mathematics and computer science
Department of Mathematics
Email: naziha.belmahi@univ-usto.dz

-
Ce cours vise à fournir une compréhension approfondie des équations différentielles fractionnaires et de leurs applications. Tout d'abord, nous introduirons les concepts fondamentaux des intégrales et dérivées fractionnaires selon les approches de Riemann-Liouville, Caputo et Grandwall. Nous explorerons ensuite les propriétés spécifiques de ces dérivées fractionnaires, y compris leur comportement et leurs applications pratiques.
Un autre objectif essentiel est de présenter une classe d'équations différentielles fractionnaires. Pour être en mesure de résoudre efficacement ces équations, ce cours couvrira également différentes méthodes de résolution, qu'elles soient analytiques ou numériques. A la fin de ce cours, une solide compréhension des dérivées fractionnaires sera acquise, l'étudiante va être capable de reconnaître et de résoudre des équations différentielles fractionnaires, et être prêt à appliquer ces connaissances dans des contextes variés, tels que la modélisation de phénomènes complexes en sciences, ingénierie et plus encore.
-

-
-
Découvrez une introduction simple aux dérivées fractionnaires et leurs applications dans cette vidéo informative intitulé "Riemann-Liouville Fractional Integral and Derivative: A Simple Overview". Les dérivées fractionnaires sont un concept mathématique fascinant qui permettent d'explorer les changements non entiers. Cette vidéo vous guidera à travers les bases de ce sujet complexe.
-
-
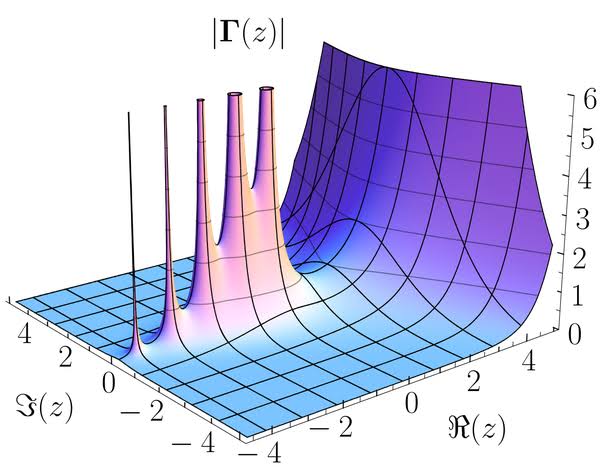
Dans ce chapitre, nous allons étudier les propriétés de certaines fonctions spéciales qui ont des propriétés intéressantes et utiles en physique, en mécanique, en ingénierie et dans d'autres domaines scientifiques. Elles apparaissent fréquemment dans la résolution d'équations différentielles et d'autres problèmes mathématiques complexes. Plus précisément, nous allons nous concentrer sur les fonctions Gamma d'Euler, Beta et Mittag-Leffler.
-
Chapitre1 ملف PDF
-
-
Les operateurs d'intégration et de dérivation fractionnaires de Riemann-Liouville sont des généralisations des operateurs d'intégration et de dérivation classiques `a des ordres non entiers. Ces operateurs ont des applications importantes dans divers domaines scientifiques. ils ont des propriétés intéressantes, telles que la linéarité, la règle de Leibniz et le théorème fondamental du calcul. Ils peuvent être utilises pour résoudre des équations différentielles fractionnaires et pour modéliser des phénomènes physiques complexes.
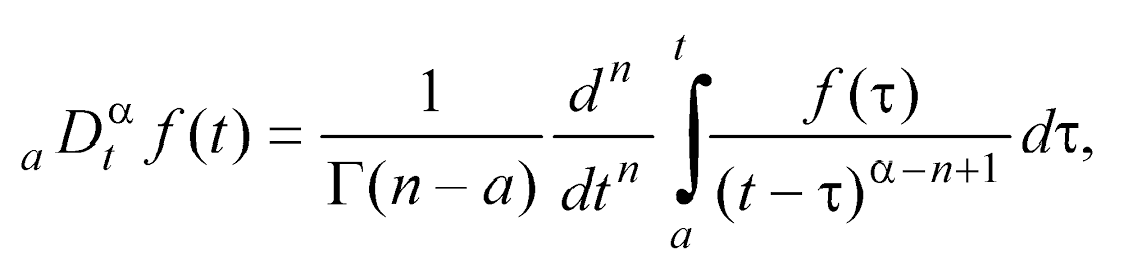
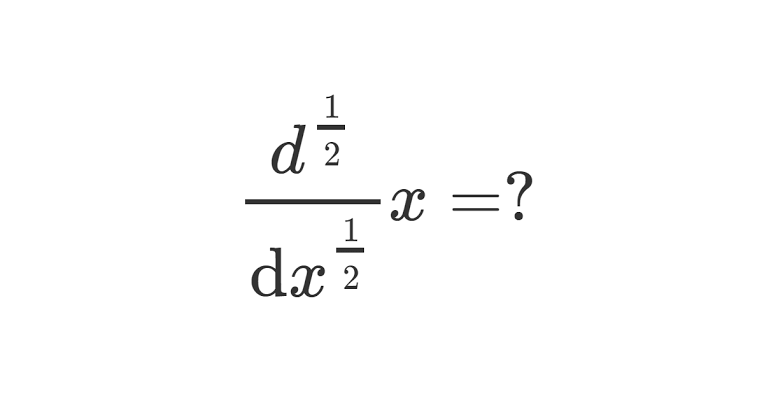
-
Chapitre2 ملف PDF
-
-
La dérivée fractionnaire au sens de Caputo est une autre généralisation de l’opérateur de dérivation classique à des ordres non entiers. Cette dérivée possède également des propriétés intéressantes, telles que la linéarité, la règle de Leibniz et le théorème fondamental du calcul. Elle peut être aussi utilisée pour résoudre des équations différentielle fractionnaires avec des conditions initiales ou des conditions aux limites non locales.
En comparaison avec la dérivée fractionnaire de Riemann-Liouville, la dérivée fractionnaire de Caputo est souvent préférée car elle est mieux adaptée à la modélisation des phénomènes physiques réels, et elle permet d’obtenir des solutions plus régulières. Cependant, la dérivée fractionnaire de Caputo est plus difficile à calculer en pratique que la dérivée fractionnaire de Riemann-Liouville.
-
Chapitre3 ملف PDF
-
Exercices ملف PDF
-
-
Les équations différentielles fractionnaires sont des équations qui impliquent des dérivées d’ordre non entier. Elles peuvent être utilisées pour modéliser des phénomènes physiques tels que la diffusion et la conduction thermique, ainsi que pour d’autres applications en sciences et en biologie. Les méthodes de résolution pour les équations différentielles fractionnaires sont similaires `a celles utilisées pourles équations différentielles ordinaires, mais avec des techniques supplémentaires pour traiter les dérivées fractionnaires. Dans ce chapitre, quelques méthodes courantes de résolution des équations différentielles fractionnaires sont présentés.
-
Chapitre4 ملف PDF
-
-
Cette section propose un examen afin de vérifier la compréhension des étudiants.

-
Exam ملف PDF
-
Rattrapage ملف PDF
-



