Résumé de section
-
In this comprehensive course on linear algebra, we will pass through a series of fundamental mathematical concepts, each building upon the last to form a solid foundation in this field of mathematics.
We will begin in the first chapter by delving into the realm of logical reasoning, providing the essential tools needed to understand the intricacies of linear algebra such as logical propositions, mathematical quantifiers and logical reasoning for proofs.
Then, we pass to the fundamental preliminaries about the applications and sets in the second chapter, demonstrating how linear algebra plays a pivotal role in solving real-world problems across various disciplines.
As we progress, we will dive into the captivating domain of relations in the third chapter, with a particular focus on equivalence relations and order relations. Understanding these concepts is crucial as they form the basis for many advanced mathematical structures.
In the fourth chapter, we will explore algebraic structures, including groups and homomorphisms of groups, rings, and fields. These abstract structures will challenge and expand our understanding of algebra, paving the way for more complex mathematical reasoning.
Finally, we will pass to the polynomials, where we will uncover their significance and applications in a multitude of mathematical and scientific contexts.
By the end of this course, you will have gained a comprehensive understanding of linear algebra, from its logical underpinnings to its diverse applications, equipping you with a powerful mathematical toolkit for your academic and professional endeavors. So, let’s embark on this intellectual voyage together, as we unravel the beauty and depth of linear algebra.
-
Linear Algebra 1, course for undergraduate
students of mathematics.
Semester : 01
Coefficient : 03
Credit : 05
The course is programed for the students
Tuesday at 8h.

-
Dr. Belmahi Naziha
University of science and technology Oran MB
Faculty of mathematics and computer science
Department of Mathematics
Email: naziha.belmahi@univ-usto.dz

-
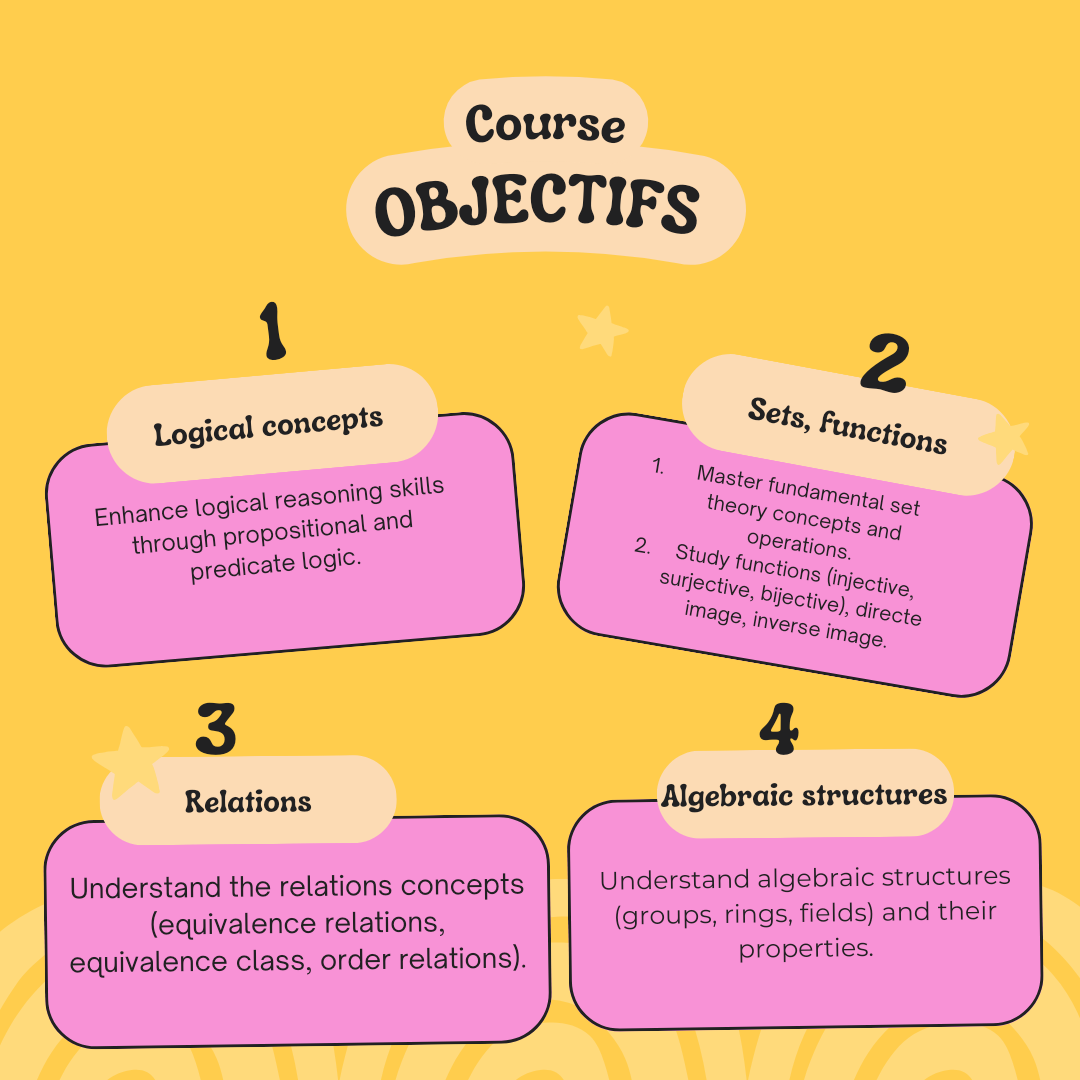
Find in this section an attached .pdf, outlining the course objectives about the linear Algebra 1 course for students specializing in mathematics. The course is designed to provide first-year mathematics students with a solid foundation in the fundamental concepts of linear algebra. Throughout the course, students will explore topics such as logic concepts, sets and functions, binary relations, algebraic structures and polynomials ring.
By the end of the course, students will have a deep understanding of linear algebra and be able to apply these principles to a wide range of disciplines, making it an essential stepping stone in their mathematical journey.

-
In this section, I'm providing you with the course plan for Linear Algebra 1, designed specifically for first-year mathematics students. Enclosed within the following plan is a comprehensive syllabus, complete with a meticulously structured schedule detailing the specific skills and topics to be covered throughout the course.
1 Logic Concepts
1.1 Assertions (Propositions)
1.2 Mathematical Quantifiers
1.3 Logical reasoning for proofs
2 Sets and applications
2.1 Definitions
2.2 Functions and Applications
3 Relations
3.1 Generalities of relations
3.2 Representation of a binary relation
3.3 Properties of a Binary Relation on a Set
3.4 Equivalence Relation
3.5 Order Relation
4 Some algebraic structures
4.1 Laws of internal composition
4.2 Groups
4.3 Ring Structure
4.4 Field Structure
5 Polynomials ring
5.1 Construction of polynomials ring
5.2 Arithmetics of polynomials
5.3 Polynomial squares, degree and multiplicity

-

-
An excellent boob for Algebra1
-
This book is a good references for the course of linear algebra 1.
-
This book covers the fundamental concepts of algebraic structures.
-
-
In terms of "linear algebra1" for undergraduatestudentsofmathematics, some necessary prerequisites are needed. A strong mathematical background and readiness for abstract thinking are key prerequisites for success in this course.

-
A short interesting video by "Gilbert Strang", a professor of mathematics in MIT.
-
In this chapter, we delve into the realm of logical concepts, providing the essential tools needed to understand the intricacies of linear algebra such as logical propositions, mathematical quantifiers and logical reasoning for proofs.
-
Welcome to the first test section of thiscourse! This assessment will gauge your comprehension and application of the first chapter material. Best of luck!

-
Test 1 Fichier PDF
-
-
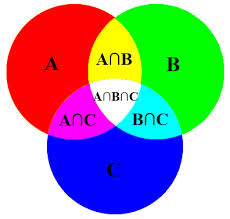
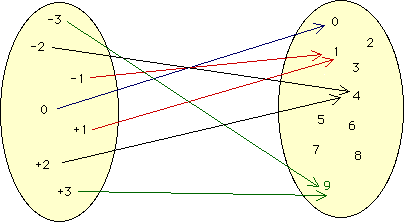
This chapter introduces fundamental concepts of sets, elements, subsets, and set operations (union, intersection, complement) that are frequently used in linear algebra, it focuses also on functions and mappings, including injective, surjective, and bijective functions. It explores the composition of functions and the concept of reciprocal functions, which are crucial for understanding transformations and operations. Additionally, it discusses the direct and inverse images of sets under a function, providing students with the essential tools to represent and analyze mathematical relationships and functions. These concepts are fundamental for a wide range of applications in linear algebra, including linear transformations, matrix operations, and system-solving.
-
Welcome back to the test section of this course! This assessment will further challenge your understanding and retention of the course material, espicialy chapter 2. Let's see how much you've learned in the course. Good luck!
-
Test2 Fichier PDF
-
-
In this chapter, we give an interest to a fundamental concept in mathematics with wide-ranging applications in various disciplines. Relations are mathematical structures that help us understand how elements from different sets are interconnected. This chapter will provide a comprehensive overview of relations, equivalence relations, and order relations.Relations are sets of ordered pairs that establish connections between elements in different sets. They can be represented as mathematical graphs, tables, or directed graphs, making it easier to visualize and analyze relationships.In particular, We analyse the equivalence relations, which satisfy three key properties: reflexivity, symmetry, and transitivity. And order relations that come in two main forms: partial order and total order.Partial Order: Partial order relations impose a certain order on elements, while allowing for non-comparable elements.Total Order: Total order relations create a strict, linear order, ensuring all elements are comparable.As applications for these concepts, relations help classify elements in set theory, enabling us to analyze set structures and relationships between elements.
-
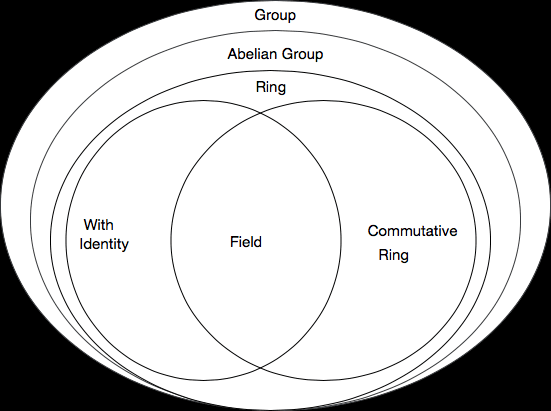
In this chapter, we introduce fundamental mathematical frameworks crucial for understanding the behavior and relationships within algebraicstructures.
This chapter delves into essential concepts like groups, subgroups, and group homomorphisms, elucidating their roles in representing transformations and symmetries. Furthermore, it explores rings, subrings, and ring homomorphisms, illustrating their coming significance in studying structures like matrices and polynomials. Finally, the chapter culminates in the exploration of fields, pivotal in defining spaces where arithmetic operations are well-defined.
-
Polynomial rings, denoted as R[x], extend the concept of rings by incorporating polynomials with coefficients from a given ring R. These algebraic structures are essential in abstract algebra, enabling operations on polynomials and finding applications in areas like algebraic geometry and computer science.
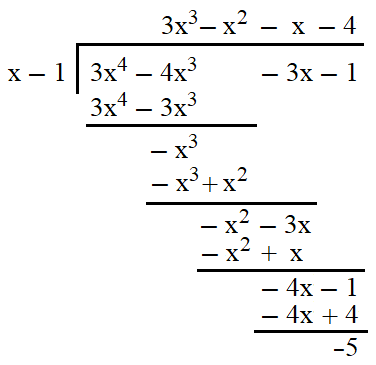
-
-
Exam Fichier PDF


