Section outline
-
This linear algebra course emphasizes key aspects of vector spaces, matrices, and linear applications. Students will delve into the fundamental properties of vector spaces, understanding their structure and identifying subspaces. Matrices take center stage, with a focus on operations such as addition, multiplication, and inversion. Linear transformations, represented through matrices, will be explored, highlighting their significance in various contexts. The course aims to provide a solid foundation in these crucial elements, enabling students to apply these concepts effectively in problem-solving scenarios and real-world applications.

-
Algebra 2, course for undergraduate students of mathematics Licence 1.
Semester : 02
Coefficient : 02
Credit : 04
The course is programed for the students
Tuesday at 11h30.

-
Dr. Belmahi Naziha
University of science and technology Oran MB
Faculty of mathematics and computer science
Department of Mathematics
Email: naziha.belmahi@univ-usto.dz
-
Welcome to Linear Algebra for L1 Math Students! This course aims to provide a solid foundation in linear algebra concepts tailored to Level 1 mathematics proficiency.
-
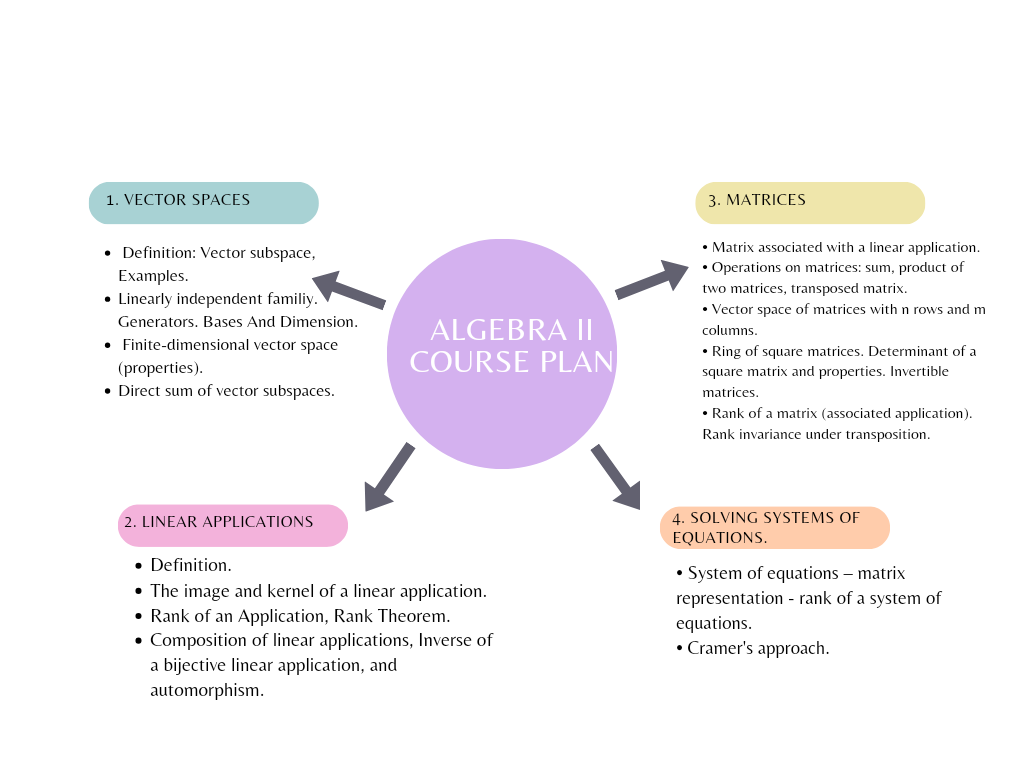
Our course plan takes you from the basics of vectors and matrices to advanced topics like solving systemsof linear equations. By course end, you'll have the skills to apply these concepts in various mathematical contexts.

-
Explore vector spaces and matrices in Algebra 2 with key references like "Linear Algebra Done Right" by Sheldon Axler, and "Linear Algebra and Its Applications" by David C. Lay.

-
Vector spaces are mathematical structures with vectors, closure under addition and scalar multiplication. Key properties include associativity, commutativity, and existence of identities. Linear independence, spanning sets, bases, and dimensionality are essential concepts to be explored in this chapter.
-
This chapter introduces linear applications, including their image and kernel, linear applications and bases, the fundamental theorem of linear mappings, and their rank. Through these fundamental concepts, students gain insights into practical applications of linear algebra across diverse fields.
-
Matrices are arrays of numbers organized into rows and columns. They're essential tools in mathematics and numerous fields, used for solving equations, representing transformations, and analyzing data.

-
This chapter covers systems of linear equations, focusing on solving multiple linear equations. Two common methods are Cramer's Rule, which uses determinants for square, invertible matrices, or the Gauss-Jordan Method, which reduces the augmented matrix to RREF for solutions.

-
Chpater 4 File PDF
-
-
Attached in this section a final exam that covers the key topics presented above. Good Luck!
-
Final Exam File PDF
-
